
zhugeduck MIT Battlecode 2024 Postmortem
Back in January, I participated in MIT Battlecode 2024. It took me a while to write this postmortem, but here we are 4 months later, let's do this.Table of Contents
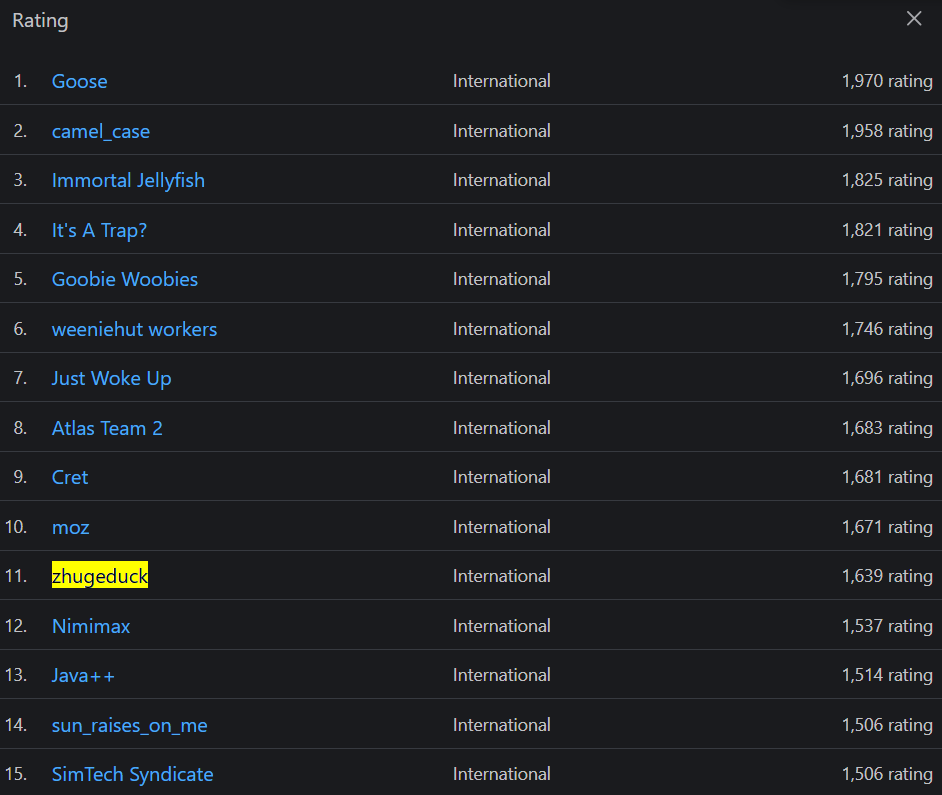
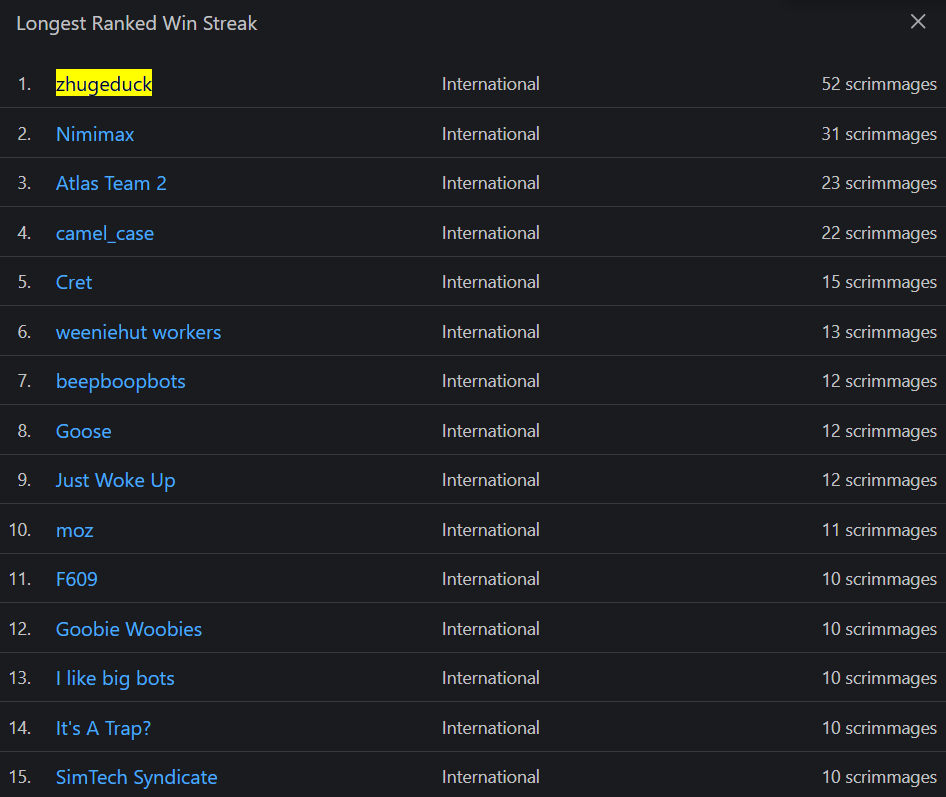
We picked the name zhugeduck because we were watching too much "Tales of the Three Kingdoms" at the time, and were inspired by the legendary general, Zhuge Liang. We also like ducks, hence the combination.By the end of the qualification period, we ranked 7th out of 100+ international teams and 31st out of 300+ teams overall. This unfortunately wasn't enough for us to qualify for the final tournament. However, we are still proud to say that we have reached a significant 1749 ELO rating, as well as the longest winning streak of all the competition. Some further statistics can be found here thanks to Jasper Van Merle
This year's game
TL;DR
Further specifications of the game can be found on the formal specification of the Battlecode 2024 gameSetup phase
The two teams will be separated by an impassable dam during the first 200 rounds of the game. Teams will use this period to collect resources, modify the terrain, and set up defenses for their flags. After the setup phase, the dam will collapse and allow both teams to move freely.
Combat phase
Each team has 3 flags. When the game starts, flags are located at the centers of each team's three spawn zones. Any unit can pick up and place a flag at any time during the setup phase. When the setup phase ends, the new locations of the flags will become the default flag locations for the remainder of the game. If a flag is being carried, it will be automatically dropped at the robot's location. Default flag placements must be a minimum distance of $\sqrt{36}$ units apart on the map. If two flags are less than this distance apart at the end of the setup phase, all flags for the team will be teleported back to the spawn zones, which will become their default locations.
Maps
The map is a discrete 2-dimensional rectangular grid of size ranging between $30 \times 30$ and $60 \times 60$ inclusive. Each team has 3 spawn zones, which are $3 \times 3$ in size and pre-placed on the map. Walls may be sparingly scattered around the map and will be impassable to either team's robots. Walls will remain fixed throughout the game and cannot be destroyed. Patches of water may also be scattered around the map. These tiles are also impassable by default, but can be built over using the fill action. Water can also be created by performing the dig action.
Units
All ducks have 1000HP and can move in each of 8 directions. Each duck must be manually spawned from one of the team's spawn zone. When it perform one of the actions (dig, fill, attack, heal), it will accumulate scores. Ducks with enough scores will be able to evolve into a more powerful unit. If the duck is killed, then it will be "jailed" for 25 rounds and must be manually spawned again.
Resources
Bread is the primary resource in the game. Bread can be collected by ducks and used to spawn new ducks, evolve ducks, and perform other actions. Bread can be accumulated during the setup phase or at a rate of 10 crumbs during the rest of the game.
Communication
Ducks in the same team cannot communicate with each other directly. Instead, each team is given a shared memory that can be read and written to by all ducks on the team. The shared memory is an array of 64 non-negative integers, each of which can be in the range $[0, 2^{16}-1]$.
Traps Your team can place traps to help defend your flags. No friendly traps are triggered by friendly units. Friendly traps can be sensed, but enemy traps are invisible Winning
The game is won by the team that captures all of the opponent's flags. If the game reaches 2000 rounds, the team with the most flags will win.
Illustrated below is one game of zhugeduck (1739)
vs Blown Up Tractors (1714) in the qualification round.
zhugeduck (white) won by capturing all of the opponent's flags after 750 rounds.
Our Strategy
Exploration
Given that the map is symmetric, it is important that we take advantage of this symmetry to reduce the number of computations needed. Understanding the border of the territories, as well as the locations of the flags, is crucial for developing an effective strategy.During the first phase of the tournament, we implemented a mutual repulsion strategy. That means the ducks, like electrons, will repel each other when they get too close. This strategy was effective in preventing ducks from clustering together and getting stuck in corners.
This strategy is actually great for the early statges of the tournament, where the maps are relatively simple with few obstacles and corners. However, one of the drawbacks of this strategy is that the ducks tends to oscillate around their "stability" points, which hinders exploration in big maps where the flags are far apart and there are "dead" corners.
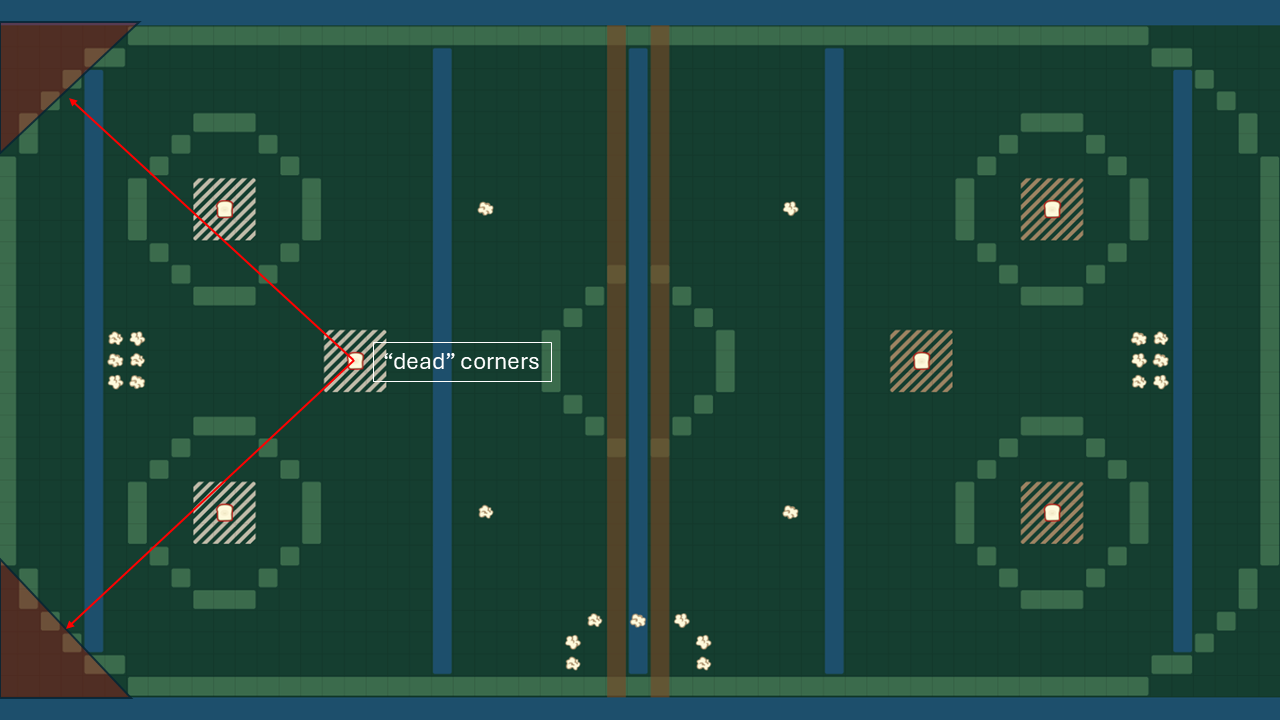
Another strategy we used in the earlier phase of the tournament but eventually decided against it was the "testudo" formation. This formation, inspired by the Roman military formation, is a defensive formation where the ducks behind the lines will engage in and develop mastery in healings and building traps, whilist the ducks in the front lines will engage in combats. This strategy was effective for quite some time and helped us to climb to 1500 ELO. But as our opponents get stronger and make more informed attacks (other than blindly stabbing the nearest enemy), this strategy became less effective.
Illustrated below is one game of zhugeduck (1553)
vs camelcase (1983) in a scrimmage.
camelcase (brown) won by capturing all of the opponent's flags after 400 rounds.
Notice that as the wall falls down, while our ducks struggle to push forward, the opponent's ducks on the 2 flanks wraps around and "backstab" the ducks in the middle. This is very disadvantageous, because only the ducks on the frontline can engage in attacks, and since a circle with larger radius has larger circumference, more enemy ducks are attacking fewer of our ducks.
Comparing this strategy with the flat formation implemented a few days later on the same map, it is evident that the flat formation is more robust and exert more pressure on the opposing team.
Illustrated below is one game of zhugeduck (1703)
vs JDK? More like IDK (1710) in a scrimmage.
camelcase (brown) won by capturing all of the opponent's flags after 400 rounds.
Intereactions
Inspired by Sun Tzu's Art of War, we developed a strategy that focused on defense, resource management, and adaptability. That is, we aimed to build a strong defense to protect our flags, while avoiding unnecessary combats with the opponent. One of the key methods we used to decide whether to engage in combats is the Lanchester's Attrition Law, which states that the rate of attrition is proportional to the product of the forces involved. The Law can be stated as follows:Definition 1: Lanchester's Attrition Law
Given two forces $A$ and $B$, the rate of attrition of each force is proportional to the product of the forces involved. $$\frac{dA}{dt} = -\alpha A$$ $$\frac{dB}{dt} = -\beta B$$This information is important, because a 6 v. 7 combat may result in a 1-deficit for the losing team, but a 24 v. 25 combat may result in a 7-deficit for the losing team, about a fourth of the battalion. We then use this information to decide whether to engage in combats with the opponent. If the opponent has a larger force, we avoid combats and focus on placing traps and healing our ducks; vice versa.
Communications
As mentioned earlier, ducks in the same team cannot communicate with each other directly. Instead, each team is given a shared memory that can be read and written by every individual duck per iteration. We used this shared memory to store information about the map, such as the locations of the flags, the number of allies and enemies in each zone, and the danger levels of each flag.There are a total of $64 \times 16 = 1024$ bits of memory available for each team. For our implementation, we used a total of $900$ bits, which is not the most rigorous and exploitative use of memory, but it leaves us with some room for improvements and auxiliary messages.
Here is the summary of what Comms stores now:
- Bot ID (6 bits)
- Possible map symmetries (3 bits, 1 for each symmetry)
- Flag danger levels (3 bits, 1 for each flag)
- Ally flag locations (12 * 3 = 36 bits)
- Enemy flag locations (12 * 3 = 36 bits)
- Zone info: we divide the map into a 10x10 grid of rectangular zones. For each of the 100 zones, we store:
- Number of allies (2 bits)
- Number of enemies (2 bits)
- Number of traps (2 bits)
- When the zone was last updated (3 bits)
Pathfinding
One of the trickiest and most important parts of the game is pathfinding, since the bytecode is limited and the map is constantly changing, making queries to the pathfinding algorithm is expensive. We used a combination of Bellman-Ford and A* algorithms to find the shortest path between two points.Definition 2: Bellman-Ford Algorithm
Bellman-Ford is a single source shortest path algorithm that determines the shortest path between a given source vertex and every other vertex in a graph. This algorithm can be used on both weighted and unweighted graphs.The Bellman-Ford algorithm’s primary principle is that it starts with a single source and calculates the distance to each node. The distance is initially unknown and assumed to be infinite, but as time goes on, the algorithm relaxes those paths by identifying a few shorter paths. Hence it is said that Bellman-Ford is based on “Principle of Relaxation“.
Now one query to the get the vision range of each duck is about 100 bytecodes, that makes pathfinding for 50 ducks at least 5000 bytecodes, not to mention those bytecodes used in processing that information. Therefore, we proposed an improved algorithm that can parallelize the procedure to process pathfinding with about 3000 bytecodes. This algorithm was also previously used in the 2022 competition, and we found it to be very effective.
We note that it is possible to parallelize one iteration of Bellman-Ford path distance calculation to process all the 69 nodes within vision range 20 using about 100 bytecodes. With $\approxeq$ 1k bytecode of wall sensing calls, $\approxeq$ 1k bytecode (10 iterations) of Bellman-Ford distance calculations, and $\approxeq$ 500 bytecode path reconstruction from distances, one can compute the shortest path between the robot position and any point within vision range out of all length $\le$ 10 paths of any shape.
This technique is centered around the idea that a 32 bit integer can be treated as a $3 \times 9$ grid of booleans (with 5 extra bits to discard), such that 3 integers can model a boolean array covering every tile within vision range. In this representation, boolean operations and spatial translations can be performed in parallel by bitwise operations and bitshifts respectively. Then to run one iteration of Bellman-Ford, one begins with a boolean array indicating which nodes are reachable on iteration $i$, convolves this with a $3 \times 1$ vertical kernel and then a $1 \times 3$ horizontal kernel, and finally bitmasks with an passability array, to obtain a new boolean array indicating which nodes are reachable on iteration $i+1$. The final path reconstruction is performed by greedy descent on the 10 resultant boolean arrays using large switches and conditionals.
Spawning, Defending, and Capturing Flags
Spawning
In retrospect, one of our key weaknesses was our inability to spawn ducks quickly and efficiently. This is due to the difficulties in balancing between attacking and defending. It is very easy to notice one of our flag is being attacked, by sensing the number of enemies in the vicinity of the flag. However, it is much more difficult to sense enemies that are rushing to the flag, and whether they are further or closer to our spawn zones. Therefore, instead of a reactive strategy, we spawned the ducks at the nearest point to its death, with the assumption that the duck fell at the "hot spots".Defending
We also implemented a strategy to defend our flags by placing traps around the flags. Traps are invisible to the opponent and can be used to catch enemy ducks that are trying to capture our flags. We also used traps to block enemy paths and prevent them from reaching our flags. We utilized a lot of water traps to block the enemy's path. Though the traps will vary from year to year, the general idea is to use cheap traps and place as many as possible to confuse the enemies' pathfinding algorithm. Evidently, lots of ducks in weaker teams (1500-1750) were caught in ponds and couldn't escape.
Illustrated below is one game of zhugeduck (1718)
vs Blown Up Tractors (1711) in a scrimmage.
zhugeduck (white) won by capturing all of the opponent's flags after 800 rounds.
Even though Blown Up Tractors have captured BOTH of zhugeduck's remaining flags,
they were unable to rush home as the flag carriers were confused by the vast pond ahead.

Capturing Flags
Once our ducks sense and confirm the location of an enemy flag, they will rush to the flag and attempt to capture it. Since the game is win by capturing the oponent's flag, the ducks act most aggressively when they sense that the enemy is weak and vulnerable. (i.e. they must capture the flag at all costs, while hoping that the defenders are weak and the allies arrive in time).One of our key improvement to the capturing strategy is the use of the "pass and run" strategy. This haven't been implemented by any other team in the competition, but it has proven key to our success in the game. The idea is that if the duck sense an ally that is closer to home, it will pass the flag to the ally and both ducks will run back to the base. This idea has 2 advantages:
- The flag is passed to a duck that is closer to the base, which means that the flag will be captured faster
- The flag passer will now become a defensive line to the flag carrier, which means that the flag carrier will be safer
Illustrated below is one game of zhugeduck (1738)
vs moz (1701) in a scrimmage.
zhugeduck (white) won by capturing all of the opponent's flags after 800 rounds.
The white ducks not only used the pass and run strategy to quickly capture the flags, but also to quickly overcome
obstacles by "throwing the flag" to the other side of the pond/wall.